Теория игр: концепции решений и равновесия 🎲

💼 Спонсор публикации: украинский криптовалютный обменник BTC/UAH - BtcBank >>>

В "Дилемме заключенного" результат, который мы представили как 2,2 (указывающий на взаимное сознание арестантов), был назван "решением" игры. Следуя общей экономической практике, теоретики игр называют решения игр равновесиями.

Самостоятельно мыслящие читатели захотят уже в этом месте задать концептуальный вопрос: что именно должно быть "уравновешено" в некоторых результатах игры, чтобы иметь полное право называть подобные итоги "решениями"?

Когда мы говорим, что физическая система находится в равновесии, то имеем в виду, что она находится в стабильном состоянии, в котором все внутренние причинные силы системы уравновешивают друг друга и, таким образом, оставляют её в "состоянии покоя" - до тех пор, пока она не будет снова возмущена вмешательством какой-то экзогенной (то есть внешней) силы. Это то, что традиционно имели в виду экономисты, говоря о "равновесии": они воспринимают экономические системы как сети взаимно ограничивающих (часто причинно-следственных) отношений, как и физические системы - и тогда равновесия таких систем являются их эндогенно-стабильными состояниями (обратите внимание, что как в физических, так и в экономических системах, эндогенно-стабильные состояния могут никогда не наблюдаться напрямую, потому-что рассматриваемые системы никогда не изолированы от внешних воздействий, которые в реальных условиях постоянно влияют и дестабилизируют их).

Как в классической механике, так и в экономике, концепции равновесия являются инструментами для анализа, а не предсказания того, что мы ожидаем получить. При дальнейшем изучении станет ясно, что можно сохранить такое понимание равновесия и в случае Теории игр. Однако, как уже было отмечено в предыдущих статьях, некоторые люди интерпретируют Теорию игр как объяснительную теорию стратегических рассуждений. Для них решение игры должно быть результатом, который рациональный агент мог бы предсказать, используя только механизмы рациональных вычислений. Такие теоретики сталкиваются с некоторыми загадками, связанными с концепциями решения, которые менее важны для теоретика, который не пытается использовать Теорию игр для подобного замещения ею общего рационального анализа.
Интерес к Теории игр на основе именно такой мотивации встречается чаще у философов, чем у экономистов или других учёных.

Полезно начать обсуждение равновесия с примера уже затронутой Дилеммы заключённого, потому-что она необычайно проста с точки зрения головоломок о концепциях решения. То, что мы назвали её "решением", по Нэшу является уникальным равновесием в игре.

Прим.: Джон Форбс Нэш-младший - математик, лауреат Нобелевской премии, который внёс большой вклад в расширение и обобщение новаторской работы фон Неймана и Моргенштерна. Равновесие Нэша (далее "РН") применимо (или не применяется, в зависимости от обстоятельств) для целых наборов стратегий - по одной для каждого игрока в игре.

Набор стратегий даёт РН в том случае, если ни один игрок не сможет улучшить свой выигрыш, учитывая стратегии всех других игроков, и изменив свою стратегию. Обратите внимание, насколько тесно эта идея связана с идеей строгого доминирования: ни одна стратегия не может быть стратегией РН, если над ней строго доминируют. Следовательно, если итеративное исключение строго доминируемых стратегий приводит нас к уникальному результату, мы знаем, что вектор стратегий, который приводит к нему, является уникальным сетевым элементом игры. Теперь почти все теоретики согласны с тем, что избегание строго доминируемых стратегий является минимальным требованием экономической рациональности. Игрок, который сознательно выбирает стратегию со строгим доминированием, напрямую нарушает базовые экономические принципы (а, точнее, писанные правила). Это означает, что если игра имеет результат, который является уникальным РН, как в случае совместного сознания в Дилемме заключённого, такой вариант должен быть её уникальным решением. Это один из наиболее важных аспектов, из-за которого ДЗ является "лёгкой" (и нетипичной) игрой.

Можно указать один класс игр, в которых РН всегда не только необходимо, но и достаточно в качестве концепции решения. Это конечные игры с идеальной информацией, которые также являются играми с нулевой суммой.

Игра с нулевой суммой (в случае игры с участием всего двух игроков) - это игра, в которой один игрок может стать лучше, только ухудшив положение другого игрока (крестики-нолики - простой пример такой игры: любой ход, приближающий одного игрока к победе, приближает его оппонента к проигрышу, и наоборот).

Мы можем определить, является ли игра - игрой с нулевой суммой, исследуя "Функции полезности" игроков: в играх с нулевой суммой они будут зеркальным отражением друг друга, при этом результаты одного игрока с высоким рейтингом будут давать низкий рейтинг для другого, и наоборот. В такой игре, если я строю свою стратегию, с учётом Вашей стратегии, я не могу добиться большего, если Вы также играете, опираясь на подобную стратегию. Поскольку любое изменение стратегии мной должно заставлять Вас перестраиваться, и наоборот, из этого следует, что наша игра не может иметь никакого решения, совместимого с нашей взаимной экономической рациональностью, кроме её уникального РН. Можно выразить это и по-другому: в игре с нулевой суммой, при моей стратегии, которая максимизирует мой минимальный выигрыш, если Вы играете как можно лучше, и одновременно делаете то же самое, что и я, это просто эквивалентно тому, что мы оба играем в наши лучшие стратегии. Таким образом, эта пара так называемых "максимальных" процедур гарантированно найдет единственное решение игры, которое является её единственным сетевым элементом (в крестиках-ноликах это будет ничья. Вы не можете сделать ничего лучше, чем затащить на ничью, и я также - если мы оба достаточно умны [по крайней мере для уровня этой простейшей игры] и оба стараемся выиграть).

Однако в большинстве игр такого свойства нет. В этой статье не удастся перечислить все возможные проблемы с играми с точки зрения их возможных решений (априори маловероятно, чтобы теоретики обнаружили все возможные проблемы). Тем не менее, мы можем попытаться их обобщить, насколько это возможно.

Во-первых, существует проблема, заключающаяся в том, что в большинстве игр с ненулевой суммой существует более одного сетевого элемента, но не все сетевые элементы выглядят одинаково правдоподобно, как решения, к которым могут обратиться стратегически бдительные игроки. Рассмотрим игру в стратегической форме, представленную следующей матрицей, взятой из работы Девида Крэпса "Курс микроэкономической теории" (университет Принстона):

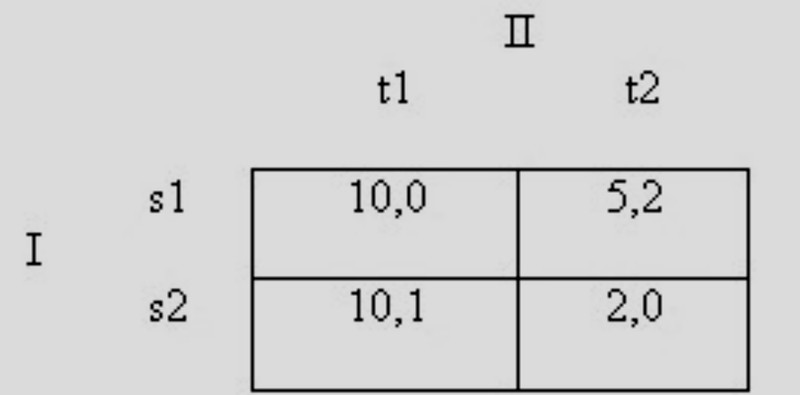
Здесь ни одна стратегия строго не доминирует над другой. Однако верхняя строка Игрока I, s1, слабо доминирует над s2, поскольку I по крайней мере так же хорошо использует s1, как s2 для любого ответа Игрока II, а в одном ответе II (t2) лучше I. Так не должны ли игроки (и аналитик) удалить строку s2 со слабым доминированием? Когда они это сделают, тогда начинает строго доминировать столбец t1, и РН s1-t2 выбирается как уникальное решение. Однако, как показывает далее Крэпс на этом примере, идея о том, что стратегии со слабым доминированием должны быть удалены, имеет странные последствия. Предположим, мы немного изменим выплаты в игре следующим образом:

s2 по-прежнему слабо доминирует; но из двух наших РН теперь s2-t1 наиболее привлекательна для обоих игроков; так почему аналитик должен исключать эту возможность? (обратите внимание, что эта игра, опять же, не повторяет логику Дилеммы заключённого. Здесь, наоборот, имеет смысл исключить наиболее привлекательный результат - совместный отказ от сознания, потому-что у обоих игроков есть стимулы в одностороннем порядке отклониться от него, и значит это не РН. Однако сказанное не относится к s2-t1 в данной игре. Вы должны начать ясно понимать, почему мы назвали игру Дилемма заключённого "нетипичной").

Аргумент в пользу исключения стратегий со слабым доминированием состоит в том, что Игрок 1 может нервничать, и опасаясь этого, Игрок II тоже станет не совсем уверен в своей экономической рациональности (либо Игрок II будет опасаться, что Игрок I не является полностью экономически рациональным и надёжным, или Игрок II предположит, что Игрок I опасается, что Игрок II не является полностью экономически рациональным, и т. д., и т.п. - "трепание" самому себе нервов до бесконечности), и поэтому может с некоторой положительной вероятностью сыграть t2. Если серьёзно отнестись к возможности отклонений от надёжной экономической рациональности, то мы получим аргумент в пользу отказа от стратегий со слабым доминированием: таким образом игрок I застрахован от своего худшего исхода, s2-t2. Конечно, он оплачивает эту перестраховку, уменьшая свой ожидаемый выигрыш с 10 до 5. С другой стороны, мы можем представить, что игроки могут пообщаться перед игрой и согласиться играть коррелированные стратегии, чтобы координировать действия по s2- t1, тем самым устраняя большую часть (или даже всю) неопределенность, которая способствует исключению строки s1 со слабым преобладанием, и вместо этого исключая s1-t2 как жизнеспособное решение!

Любой предложенный принцип решения игр, который может привести к исключению одного или нескольких РН из рассмотрения в виде возможных решений, называется Уточнением Равновесия Нэша.
В только что обсуждённом случае устранение слабо доминируемых стратегий является одним из возможных усовершенствований, поскольку это устраняет РН s2-t1, а корреляция - это другое, поскольку вместо этого она очищает другой РН, s1-t2.

Итак, какая доработка более уместна в качестве концепции решения? Люди, считающие Теорию игр объяснительной и / или нормативной теорией стратегической рациональности, создали обширную литературу, в которой обсуждаются достоинства и недостатки большого числа уточнений. В принципе, кажется, нет предела количеству уточнений, которые можно было бы рассмотреть, поскольку также может не быть ограничений на набор интуитивных и философских предположений относительно того, каким принципам рациональный агент может (или не может) счесть целесообразным следовать или опасаться / либо надеяться, что другие игроки им последуют.

Теперь сделаем небольшое отступление и остановимся на терминологии. Теоретиков, которые принимают интерпретацию выявленных предпочтений функций полезности в Теории игр, иногда называют в философской экономической литературе "бихевиористами". Это отражает тот факт, что выявленные подходы к предпочтениям приравнивают выбор к экономически последовательным действиям, а не предназначены для ссылки на ментальные конструкции. Исторически сложилось так, что между выявленными предпочтениями в экономике и методологическим и онтологическим бихевиоризмом, доминировавшим в научной психологии в середине двадцатого века, существовала связь удобного согласования, хотя и не прямого теоретического построения. Однако такое использование всё чаще вызывает путаницу из-за дальнейшего развития поведенческой Теории игр уже в 21-м веке (напр., Camerer, 2003). Эта программа исследований была направлена на прямое включение в теоретико-игровые модели обобщений, полученных в основном из экспериментов с людьми, на основании тех нюансов, которыми живые (и эмоциональные!) люди отличаются от более чистых экономических агентов в выводах, которые они делают из получаемой информации (специфика "построения рамок"). Приложения также обычно включают специальные предположения о функциях полезности, тоже полученных в результате экспериментов. Например, игроки могут быть склонны к компромиссу между величинами своих собственных выигрышей и неравенством в распределении выигрышей между остальными игроками. Мы вернёмся к обсуждению теории поведенческих игр в последующих публикациях. На данный момент отметим, что такое использование теории игр в значительной степени основывается на предположениях насчёт психологических представлений о ценностях, которые, как считается, важны для людей. Таким образом, было бы ошибочным называть теорию поведенческих игр "бихевиористской". Если и дальше продолжать называть традиционную экономическую теорию игр, которая опирается на выявленные предпочтения, "бихевиористской" теорией игр - это будет вызывать всё большую путаницу. Поэтому мы назовём её более уместно - "Непсихологической теорией игр". Под этим подразумевается Теория игр, которую используют большинство экономистов, не являющихся ревизионистскими / бихевиористскими экономистами (мы используем квалификатор "ревизионист", чтобы отразить дальнейшее усложнение концепций по причине того, что всё больше экономистов, применяющих выявленные концепции предпочтений, проводят собственные эксперименты, и некоторые из них называют себя "поведенческими экономистами").

Новый набор определений для уменьшения такого хаоса навешивания ярлыков и понятий предложил Д.Росс в своей работе "Философия экономики" (2014).
Эти экономисты из "истеблишмента" рассматривают теорию игр как абстрактную математику стратегического взаимодействия, а не как попытку напрямую охарактеризовать особые психологические предрасположенности, которые могут быть типичными для реальных людей.

"Непсихологические теоретики" игр склонны без энтузиазма относиться к большей части программ усовершенствования теории. Так происходит по той очевидной причине, что они полагаются на свою интуицию относительно того, какие типы умозаключений люди должны бы считать разумными. Как и большинство учёных, непсихологические теоретики игр несколько оторваны от реальной жизни, и с подозрением относятся к силе и основанию философских допущений - как руководящих принципов эмпирического и математического моделирования.

Напротив, поведенческую Теорию игр лучше понимать как расширение Теории игр в целом, и не обязательно смотреть на неё, как на концепцию решения, в смысле какого-либо противопоставления. Она фокусирует основные аксиомы Теории игр для применения к особому классу агентов: индивидуальным или психологически типичным людям. Эта фокусировка мотивируется ссылкой на выводы, наряду с предпочтениями, которые люди действительно находят естественными, независимо от того, кажутся ли они рациональными учёным (а они часто таковыми как раз не являются!). Общее для непсихологической и поведенческой Теории игр состоит в том, что ни одна из них не является нормативной, хотя обе часто используются для описания норм, преобладающих в группах игроков, а также для объяснения того, почему нормы могут сохраняться в этих группах игроков, даже если они кажутся не очень рациональными с точки зрения философской интуиции. Оба типа теоретиков понимают, что задача прикладной Теории игр заключается в прогнозировании результатов эмпирических игр с учётом некоторого распределения стратегических диспозиций, а также распределения ожиданий относительно стратегических диспозиций других, которые формируются динамикой в среде игроков, включая институциональное давление структуры и эволюционного отбора. Поэтому давайте всё же сгруппируем "непсихологов" и теоретиков поведенческих игр вместе - т.к. они обоюдно контрастируют на фоне классических теоретиков нормативных игр.

Как мини-резюме на сегодня

Теоретики иллюстративных игр часто склонны сомневаться в том, что цель поиска общей теории рациональности вообще имеет смысл как проект. Институты и эволюционные процессы создают множество сред, и то, что считается рациональной процедурой в одной среде, может не приветствоваться в другой.
Тем более, что сущность, которая хотя бы стохастически (то есть, нередко в виде шума, и всё же чаще статистически) удовлетворяет минимальным ограничениям экономической рациональности, не может, кроме как случайно, быть точно охарактеризована в качестве стремящейся максимизировать свою функцию полезности. К таким сущностям Теория игр вообще не применима.

Это не означает, что непсихологические теоретики игр отказываются от всех принципиальных способов ограничения наборов РН до под-множеств, на основе их относительной вероятности возникновения. В частности, непсихологические теоретики игр склонны сочувствовать подходам, которые переносят акцент с рациональности на рассмотрение информационной динамики игры. Возможно, нам не следует удивляться тому, что сам по себе РН-анализ часто не может рассказать многое о прикладном, эмпирическом интересе к играм в стратегической форме, в которых подавляется информационная структура. Вопросы выбора равновесия часто более плодотворно рассматриваются в контексте игр с расширенными формами.