💼 Спонсор публикации: криптовалютная биржа EXMO >>>

Рассмотренные в предыдущей публикации отличия трудно правильно понять, если всё, что используется, - это абстрактные описания. Лучше всего проиллюстрировать эти концепции на конкретных примерах. Для этого воспользуемся одной из самых известных психологических игр, называемой "Дилемма заключенного".
Фактически, эта игра даёт понимание логики проблем, с которыми сталкивались солдаты Кортеса и Генриха Пятого (см. публикацию 1), а также агенты Гоббса, прежде чем они пришли к выводам о предпочтительности тирании. Однако по причинам, которые станут понятны немного позже, не следует воспринимать ДЗ как типичную игру - она таковой не является.
Мы используем здесь Дилемму Заключённого, как расширенный пример только потому, что она будет особенно полезна для иллюстрации взаимосвязи между играми стратегической формы и играми расширенной формы (а также, для иллюстрации взаимосвязи между одноразовыми и повторяющимися играми, которые мы будем рассматривать позже).
Название игры "Дилемма заключенного" происходит от следующей гипотетической (и при этом жизненной!) ситуации. Предположим, что полиция арестовала двух человек, которые вместе совершили вооружённое ограбление. Однако, для вынесения обвинительного приговора не хватает доказательств. Зато у полиции достаточно улик, чтобы посадить каждого арестованного на два года за угон машины, которая (возможно) использовалась при ограблении. Тогда следователь делает каждому заключенному по-отдельности следующее предложение: если Вы признаетесь в ограблении, в котором фигурирует и Ваш подельник, а он не признается, то Вы выйдете на свободу, а он получит десять лет тюрьмы. Если Вы оба признаетесь, каждый получит по 5 лет. А если ни один из Вас не признается, каждый получит по два года - за угон автомобиля.
Нашим первым шагом в моделировании ситуации с двумя заключёнными в виде игры является представление её в терминах функций полезности. Следуя общепринятому правилу, назовем заключенных "Игрок 1" и "Игрок 2". Порядковые функции полезности Игрока 1 и Игрока 2 идентичны:
- Не сесть вообще ≫ 4
- Сесть на 2 года ≫ 3
- Сесть на 5 лет ≫ 2
- Сесть на 10 лет ≫ 0
Числа в приведенной выше функции теперь можно использовать для выражения выигрыша каждого игрока в каждом из четырёх исходов, возможных в данной ситуации. Мы можем представить дилемму, стоящую перед ними обоими, в единой матрице, отражающей способ взаимодействия их отдельных выборов; это стратегическая форма их игры (где "confess" - означает сознаться, "refuse" - отрицать свою вину):
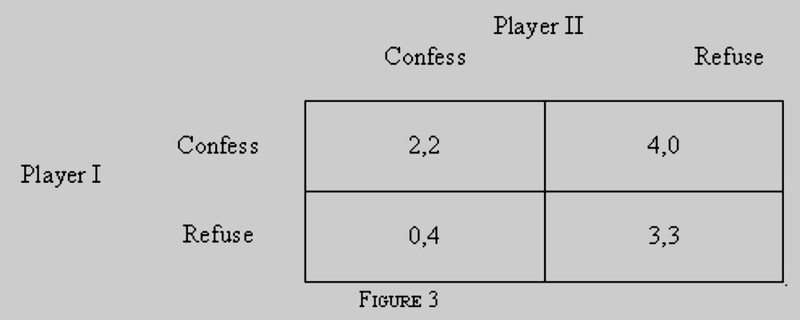
Каждая ячейка матрицы показывает судьбу обоих игроков при определённой комбинации действий. Дальнейшая судьба Игрока 1 отображается первым числом каждой пары, Игрока 2 - вторым числом (после запятой).
Итак, если оба игрока сознаются, каждый из них получает вознаграждение в размере 2 (5 лет тюрьмы каждый). Это отображается в верхней левой ячейке. Если ни один из них не сознается, каждый из них получает вознаграждение в размере 3 (по 2 года тюрьмы каждому). Это отображается в нижней правой ячейке. Если Игрок 1 сознается, а Игрок 2 - нет, то Игрок 1 получает выплату 4 (освобождение), а Игрок 2 получает выплату 0 (десять лет тюрьмы). Это отображается в верхней правой ячейке. Зеркальная ситуация, когда игрок 2 признаётся, а игрок 1 отказывается, отображена в левой нижней ячейке.
Здесь каждый игрок оценивает свои возможные действия, сравнивая свои личные выигрыши в каждом столбце, поскольку они показывают также, какое из действий предпочтительнее для каждого из возможных действий подельника. Итак, обратите внимание: если Игрок 2 сознается, то Игрок 1 получает вознаграждение в размере 2 - за сознание, и вознаграждение в размере 0 - за отрицание вины. Если Игрок 2 отказывается сознаться, то Игрок 1 получает выигрыш 4 за сознание, и выплату 3 за отказ. Следовательно, игроку 1 лучше сознаться - независимо от того, что сделает игрок 2.
Игрок 2, тем временем, оценивает свои перспективы, сравнивая свои выплаты в каждой строке, и приходит к тому же выводу, что и Игрок 1. Если одно действие игрока превосходит другие его действия для каждого возможного действия оппонента, мы понимаем, что первое действие строго доминирует над вторым. Таким образом, в Дилемме Заключённого вероятность признания вины строго преобладает над возможностью отрицания - у обоих игроков.
Более того, оба понимают это насчёт друг друга, что практически полностью исключает соблазн отклониться от наиболее вероятного выбора. Таким образом, скорее всего, оба преступника признаются, и оба отправятся в тюрьму на 5 лет.
Игроки и аналитики могут предсказать этот исход, используя механическую процедуру, известную как последовательное исключение строго доминирующих стратегий.
Игрок 1 может видеть, исследуя матрицу, что его выплаты в каждой ячейке верхней строки выше, чем его выплаты в каждой соответствующей ячейке нижней строки. Следовательно, для него никогда не может быть максимализацией полезности его стратегия нижнего ряда, независимо от того, что делает Игрок 2. Поскольку стратегия Игрока 1 по нижнему ряду никогда не будет воспроизведена, мы можем просто удалить нижнюю строку из матрицы. Теперь очевидно, что Игрок 2 не откажется сознаться, так как его выигрыш от признания в двух оставшихся ячейках выше, чем его выигрыш от отказа.
Итак, теперь мы можем удалить из игры также и столбец с одной ячейкой справа. В итоге, у нас остаётся только одна клетка, соответствующая результату сознания обоими игроками. Поскольку рассуждение, которое привело нас к исключению всех других возможных результатов, зависело на каждом этапе только от предпосылки, что оба игрока экономически рациональны, то есть будут выбирать стратегии, которые приводят к более высоким выплатам, чем стратегии, ведущие к более низким, - есть веские основания брать полученный прогноз в расчёт.
Для того, чтобы рассматривать совместное признание как решение игры, исход игры должен сходиться в той степени, в которой экономическая рациональность правильно моделирует поведение игроков.
Обратите внимание, что порядок, в котором удаляются строго доминирующие строки и столбцы, не имеет значения. Если бы мы начали с удаления правого-верхнего столбца, а затем удалили нижнюю строку, мы пришли бы к тому же решению.
Пару раз уже было сказано, что Дилемма Заключённого во многих отношениях - нетипичная игра. Одним из аспектов этого является то, что все её строки и столбцы либо строго доминируют, либо строго сдают. В любой стратегической игре, где это верно, повторное исключение строго доминирующих стратегий гарантированно даст уникальное решение. Позже, однако, мы увидим, что во многих играх это условие не работает, и тогда наша аналитическая задача становится более сложной.
Читатель, вероятно, заметил кое-то печальное в результатах Дилеммы Заключённого. Ведь если бы оба игрока отказались сознаться, они пришли бы к результату в правом нижнем углу, при котором оба попадают в тюрьму всего на 2 года, тем самым получая выгоду для обоих выше, чем когда каждый из них признаётся. Это самый важный вывод по Дилемме Заключённого, и его значение для Теории игр весьма далеко идущее. Поэтому мы ещё вернемся к нему позже, когда будем обсуждать концепции равновесия в Теории игр. А пока давайте остановимся на использовании этой конкретной игры, чтобы проиллюстрировать разницу между стратегической и расширенной формами игр.
Когда люди применяют ДЗ в популярных дискуссиях, часто можно услышать, как они говорят, что инспектор полиции должен запирать заключенных в разных комнатах, чтобы они не могли общаться друг с другом. Обоснование этой идеи кажется очевидным: ведь если бы игроки могли общаться, они наверняка бы обговорили, что каждому из них будет лучше, если оба они откажутся от признания, и могли бы договориться о таком варианте действий, не так ли?
Такое решение, как можно предположить, сняло бы убеждение каждого игрока в том, что он или она должны признаться, потому-что в противном случае их партнёр будет в шоколаде, а он сам - при худшем итоге. Однако, на самом деле, эти доводы интуиции вводят в заблуждение, и интуитивные выводы в данном случае ошибочны.
Когда мы представляем ДЗ как игру в стратегической форме, мы авансом предполагаем, что заключенные не могут пытаться достичь соглашения, поскольку они выбирают свои действия одновременно. В этом случае согласие перед фактом не поможет. Если Игрок 1 убеждён, что его напарник будет придерживаться условий сделки, то он может воспользоваться возможностью уйти от ответственности, сознавшись. Конечно, он понимает, что такое же искушение возникнет и у Игрока 2... но в этом случае он снова захочет убедиться, что он не признается, поскольку это его единственный способ избежать худшего исхода. После цепи подобных переживаний и перебора вариантов, соглашение заключенных сводится к нулю, потому-что у них нет возможности добиться его соблюдения; их обещания друг другу составляют то, что теоретики игр называют "дешевым трёпом".
Но теперь предположим, что заключенные не принимают решения одновременно. То есть предположим, что Игрок 2 может сделать выбор, сперва узнав о действии Игрока 1. Это такая ситуация, которую должны иметь в виду люди, полагающие, что изоляция заключённых друг от друга принципиально важна. Теперь Игрок 2 сможет увидеть, что Игрок 1 оставался непоколебимым, когда дело дошло до выбора, и уже не нужно беспокоиться о том, что его обманут. Тем не менее, это ничего не меняет, и лучше всего это сделать, пересматривая игру в развёрнутой форме. Это даёт нам возможность познакомиться с древами игр, используя подходящий для них метод анализа.
Сначала приведем определения некоторых концепций, которые будут полезны при анализе игровых древ:
- Узел: точка, в которой игрок выбирает действие.
- Начальный узел: точка, в которой происходит первое действие игры.
- Конечный узел: любой узел, при достижении которого завершается игра. Каждому конечному узлу соответствует результат.
- Под-игра: любой связанный набор ветвей и узлов, однозначно идущих от одного узла.
- Выплата: порядковый номер полезности, присвоенный игроку по его результатам.
- Результат: присвоение набора индивидуальных выплат каждому игроку в игре.
- Стратегия: программа, инструктирующая игрока, какое действие следует предпринять в каждом узле древа, в котором он может столкнуться с необходимостью выбора.
Эти краткие определения могут не иметь большого значения для Вас, пока Вы не проследите, как они используются в нашем анализе древ ниже. Вероятно, будет лучше, если Вы перечитаете несколько раз информацию выше и ниже между последующими примерами. К тому времени, когда Вы поймете каждый пример, Вы обнаружите, что концепции и их определения естественны и интуитивно понятны.
Чтобы сделать это упражнение максимально поучительным, предположим, что игроки 1 и 2 изучили приведенную выше матрицу и, поняв, что они оба получат оптимальный результат, представленный в нижней правой ячейке, всё-таки заключили соглашение о сотрудничестве (сговорились). Игрок 1 должен сначала дать отказ от показаний, после чего Игрок 2 ответит тем же, когда полиция попросит его определиться. Мы будем называть стратегию сохранения соглашения "сотрудничеством" и обозначили её на древе ниже буквой "C". Стратегию нарушения соглашения назовём "предательством" - на древе ниже обозначена буквой "D". Каждый узел пронумерован 1, 2, 3… сверху вниз - для удобства использования при обсуждении.
Итак, вот игровое древо Дилеммы Заключённого - в варианте игры с поочерёдными ходами (игроки помечены римскими цифрами, Игрок 1 принимает решение первым):
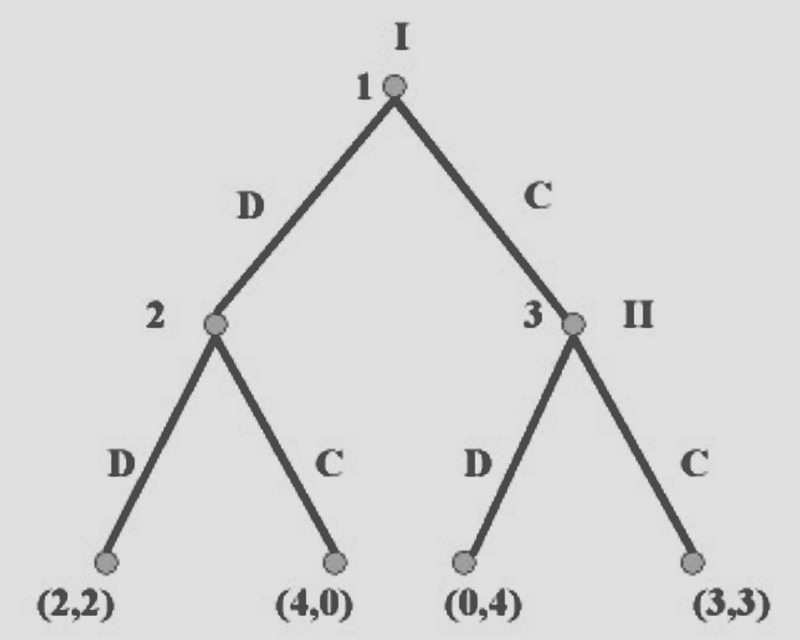
Сначала посмотрите на каждый из конечных узлов, расположенных в самом низу. Они представляют собой возможные результаты. Каждый идентифицируется со значением выигрышей, как и в стратегической игре, где выигрыш Игрока 1 появляется первым в каждом наборе, а выигрыш Игрока 2 отображается вторым, после запятой. Каждая из структур, спускающихся из узлов 1, 2 и 3 соответственно, является вспомогательной игрой. Мы проводим наш анализ обратной индукции - используя метод, называемый алгоритмом Цермело - начиная с под-игр, которые возникают последними в последовательности игры. Если играть во вспомогательную игру, идущую от узла 3, то Игрок 2 столкнётся с выбором между выплатой 4 и выплатой 3 (смотрите на второе число, представляющее его выплату, в каждом наборе в конечном узле, спускающемся от узла 3), Игрок 2 получает более высокий выигрыш, играя по стратегии D (предательство напарника). Таким образом, мы можем заменить всю под-игру назначением выплаты (0,4) непосредственно узлу 3, поскольку это результат, который будет реализован, если игра достигнет этого узла.
Теперь рассмотрим под-игру, идущую от узла 2. Здесь Игрок 2 стоит перед выбором между выигрышем 2 и одним из 0. Он получает свой более высокий выигрыш, 2, играя по стратегии D (предательство). Таким образом, мы можем присвоить выигрыш (2,2) непосредственно узлу 2.
Далее мы переходим к вспомогательной игре, идущей от узла 1 - эта вспомогательная игра, конечно, идентична всей игре (все части игры сами по себе являются под-играми). Игрок 1 теперь стоит перед выбором между исходами (2,2) и (0,4). Сверившись с первыми числами в каждом из этих наборов, он видит, что получает свой более высокий выигрыш - 2 - играя по стратегии D (предательство).
Итак, игрок 1 сознаётся, а затем игрок 2 также сознаётся, что даёт тот же результат, который получаем и при анализе в стратегической форме.
На интуитивном уровне здесь происходит то, что Игрок 1 понимает, что если он сыграет C (откажется сознаться) в узле 1, то Игрок 2 сможет максимализировать свою выгоду, предав его и сыграв D (на древе это происходит в узле 3.) Такой расклад оставляет Игрока 1 с выигрышем 0 (десять лет тюрьмы), которого он может избежать, только сыграв D с самого начала. Поэтому он сразу отклоняется от соглашения.
Таким образом, мы увидели, что в случае Дилеммы Заключенного, версии с одновременными и поочерёдными ходами дают один и тот же результат. Однако это часто не относится к другим играм. Более того, с помощью алгоритма Цермело можно решить только конечные (последовательные) игры с совершенной информацией в развёрнутой форме.
Как отмечалось ранее, иногда следует представлять одновременные ходы в играх, которые в остальном являются поочерёдными (во всех таких случаях игра в целом будет содержать несовершенную информацию, поэтому мы не сможем решить её при помощи алгоритма Цермело).
Игры, не решаемые с помощью алгоритма Цермело, можно анализировать, используя устройство информационных наборов.
Рассмотрим ещё одно игровое древо, дающее понимание этой концепции:
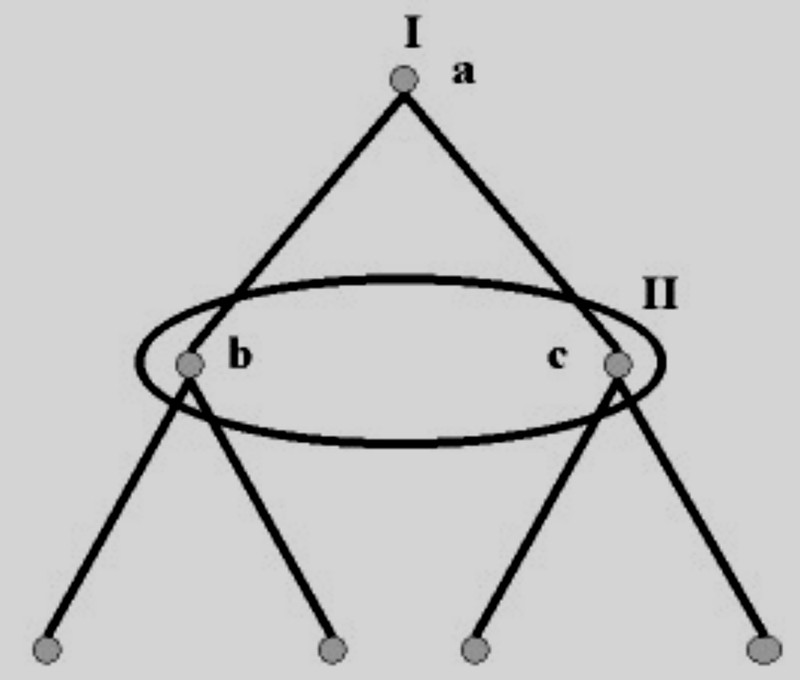
Овал, нарисованный вокруг узлов b и c, указывает на то, что эти узлы находятся в пределах общего набора информации. Это означает, что в этих узлах игроки не могут сделать вывод о пути, откуда они пришли; Игрок 2, выбирая свою стратегию, не знает, находится ли он в точке b или c (по этой причине то, что правильно помечается числами в играх расширенной формы, - это информационные наборы, задуманные как "точки действия", а не сами узлы; вот почему узлы внутри овала помечены буквами, а не числами). Иными словами. , Игрок 2 при выборе не знает, что Игрок 1 сделал в узле a. Но, как Вы помните, ранее мы обсудили: это как раз то, что определяет два хода как одновременные. Таким образом, мы видим, что метод представления игр в виде древ является полностью общим. Если ни один узел после начального узла не является единственным в информационном наборе его древа, так что в игре есть только одна вспомогательная игра (основная), тогда всю игру можно считать игрой одновременных ходов. Если же хотя бы один узел делится своим информационным набором с другим, в то время как остальные располагаются изолированно (в плане информации), тогда игра включает в себя как одновременную, так и последовательную очерёдность ходов, и поэтому всё ещё остаётся игрой с несовершенной информацией. И только в том случае, если все информационные наборы определяются одним узлом, получаем игру с идеальной информацией.
17 августа 2020 г., Богдан Карасёв, на основе материалов Стенфордского университета.
Уникальность статьи 100% (RU).
🎲 Анонс (продолжение по теме Теории игр):
Концепции решений и равновесия (материал будет добавлен в моём блоге между 19 и 26 августа 2020 г.)
Комментарии