Совершенствование под-игр 🎲

💼 Спонсор публикации: криптовалютная биржа EXMO >>>

Чтобы углубить наше понимание игр с расширенной формой, нам нужен пример с более интересной структурой, чем предлагала Дилемма заключённого.

Рассмотрим игру, описываемую следующим древом:

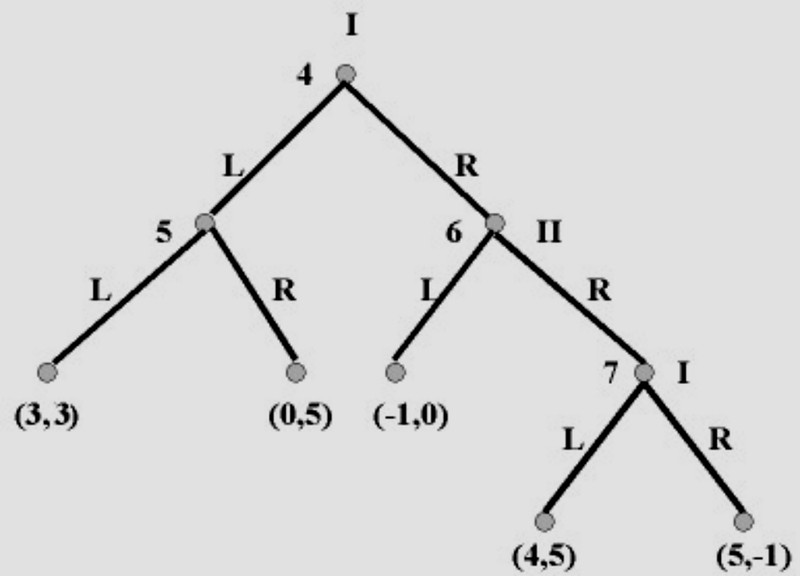
Эта игра не предназначена для использования в какой-либо предвзятой ситуации; это просто математический объект в поисках решения (L и R здесь просто обозначают "налево" и "направо" соответственно).

Теперь рассмотрим стратегическую форму этой игры:

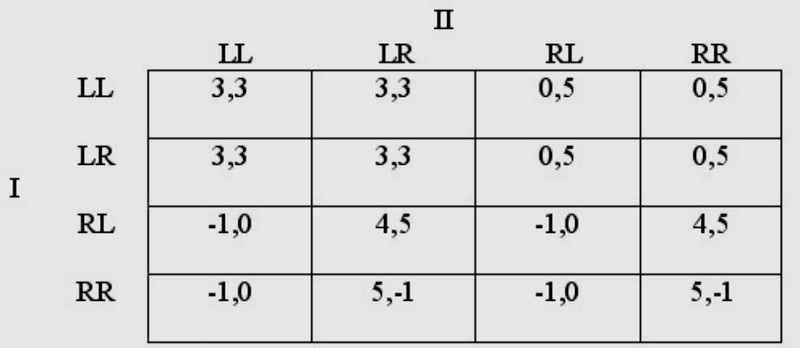
Если Вас смущает сложность таблицы, помните, что стратегия должна указывать игроку, что ему делать, при каждом информационном наборе обстоятельств, в котором этот игрок может оказаться, и должен будет выполнить действие. Поскольку выбор доступен между двумя действиями в каждом из двух наборов информации у обоих игроков может быть всего по четыре стратегии. Первая буква в обозначениях стратегии сообщает игрокам, что делать, если он или она достигают своего первого набора информации, а вторая буква - что делать, если достигается их второй набор информации. То есть, LR для Игрока II сообщает, что нужно играть L, если достигнут набор информации 5, и R, если достигнут набор информации 6.

Когда Вы изучите приведённую матрицу, то обнаружите, что (LL, RL) находится среди Равновесия Нэша (РН). Это немного сбивает с толку, поскольку если Игрок I достигнет своего второго информационного набора (7) в игре с расширенными формами, он вряд ли захочет играть L; т.к. он получает более высокий выигрыш, играя R в узле 7. Простой анализ РН не замечает этого, потому-что РН нечувствителен к тому, что происходит вне пути игры. Игрок I, выбирая L в узле 4, гарантирует, что узел 7 не будет достигнут; это то, что имеется в виду, когда говорится, что он "не на пути к игре". Однако при анализе игр с расширенной формой нам следует заботиться о том, что происходит вне игрового процесса, потому-что рассмотрение этого имеет решающее значение для того, что происходит на пути. Например, именно тот факт, что Игрок I сыграет R, если будет достигнут узел 7, заставит Игрока II играть L, если будет достигнут узел 6, и именно поэтому Игрок I не выберет R в узле 4. Мы отбрасываем информацию, относящуюся к игровым решениям, если игнорируем побочные результаты, как это делает простой анализ РН. Обратите внимание, что подобная причина сомнений в том, что РН является полностью удовлетворительной концепцией равновесия, сама по себе не имеет ничего общего с интуитивными представлениями о рациональности, как в случае концепций уточнения, рассмотренных в предыдущей публикации.

Оффтоп (пауза для юмора): фишки, коины, фантики, блондинки... ⬇️

Теперь применим алгоритм Цермело к развёрнутой форме нашего текущего примера (т.е. не к Алисе, а к игровому древу).

Снова начнём с последней под-игры, которая спускается от узла 7. Это ход Игрока I, и он выбрал бы R, потому-что он предпочтёт более высокую выплату 5, вместо выплаты 4, которую он получит, играя L. Таким образом, мы назначаем выигрыш (5, −1) к узлу 7. Соответственно, в узле 6 Игрок II стоит перед выбором между (−1, 0) и (5, −1). Он выбирает L. В узле 5 Игрок II выбирает R. В узле 4 Игрок I, таким образом, выбирает между (0, 5) и (−1, 0), и поэтому играет L. Обратите внимание, что, как и в Дилемме заключённого, результат (4, 5) появляется в конечном узле, идущем от узла 7, который по Парето выше РН. Однако, опять же, динамика игры не позволяет этого достичь.

Тот факт, что алгоритм Цермело выбирает вектор стратегии (LR, RL) как уникальное решение игры, показывает, что он даёт нечто иное, чем просто Равновесие Нэша. Фактически, он генерирует идеальное равновесие во вспомогательной игре (SPE), что приносит результат, который даст РН не только во всей игре, но и в каждой под-игре. Это убедительная концепция решения, потому-что, опять же, в отличие от уточнений статьи о равновесии, она не требует от агентов "дополнительной" рациональности в том смысле, что от них ожидается наличие и использование философских интуитивных представлений о том, "что имеет смысл". Однако она предполагает, что игроки не только знают всё, что имеет стратегическое значение для их ситуации, но и используют всю эту информацию. В спорах об основах экономики это часто называют аспектом рациональности, например, в понятии "рациональные ожидания". Но, как отмечалось ранее, лучше не путать общую нормативную идею рациональности с вычислительной мощностью и наличием бюджета, времени и энергии, позволяющими максимально использовать имеющуюся идею.

Оффтоп (пауза для юмора): Всё-таки, в жизни Теория игр - штука гораздо более интересная, чем просто при изучении. Вот и вчера на Фейсбуке, мой краткий пост с цитатой А. Савватеева по игровой теории не оставил равнодушной рыжеволосую красавицу, которая в три часа ночи подвергла меня за него неожиданной критике - зачем я, мол,такой-сякой дурак, заумными абзацами Фейсбук порчу?
Нооо...прямо как в том игровом древе с неловкими узлами, за которыми следуют порой более интересные ветви, переписка из 13 комментариев закончилась достижением равновесия:

Продолжим практическую часть.
Агент, играющий в идеальную стратегию вспомогательной игры, должен просто выбирать на каждом достижимом узле путь, который приносит ему наибольшую выгоду во вспомогательной игре, исходящей из этого узла.
SPE предсказывает исход игры на тот случай, если, проходя игру, игроки предвидят, что все они далеко зайдут.

Основная ценность анализа игр расширенной формы для SPE заключается в том, что это может помочь нам определить структурные барьеры на пути социальной оптимизации.

В нашем текущем примере положение Игрока I будет лучше, а Игрока II - не хуже, в левом узле, исходящем из узла 7, чем в результате SPE. Но экономическая рациональность Игрока I и осознание этого Игроком II блокируют социально эффективный результат.

📝 Богдан Карасёв, Scorum, 21 августа 2020 г., на основе материалов Стэнфордского университета.

✅ Уникальность статьи 100% (RU).

🎲 Анонс следующей публикации по теме Теории игр:

Об интерпретации выигрышей: мораль и эффективность в играх (материал будет опубликован в моём блоге между 23 и 30 августа 2020 г.)