💼 Спонсор публикации:
украинский криптовалютный обменник BTC/UAH - BtcBank >>>

Наше предыдущее обсуждение открыло путь к философской загадке - одной из нескольких подобных, которые до сих пор занимают умы людей, изучающих логические основы Теории игр. Эту загадку можно понять на огромном количестве примеров, но мы позаимствуем и разберём изящный пример от C. Bicchieri.
Рассмотрим следующую игру:
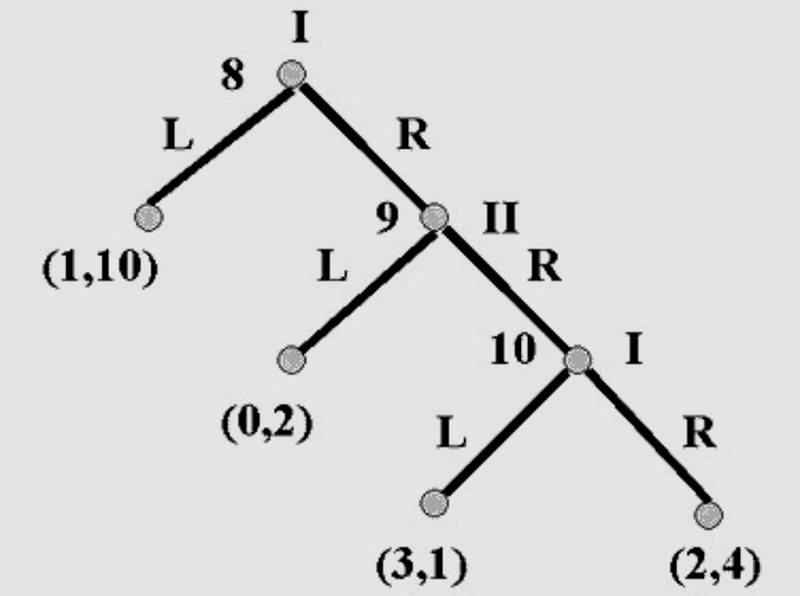
Результат с достижением равновесия Нэша (РН) здесь находится в единственном крайнем левом узле, спускающемся от узла 8 (выплаты 1,10). Чтобы увидеть это, снова выполните обратную индукцию. В узле 10 я бы сыграл L с выплатой 3, давая игроку II выплату 1. Я могу добиться и большего, играя L в узле 9, и оставляя сопернику выплату 0. Можно добиться ещё большего, играя L в узле 8; именно это я бы и сделал предпочтительнее всего - и игра закончилась бы, без возможности дальнейшего продолжения.
Затем Биккьери (вместе с другими авторами, включая Бинмора, Петтита и Сагдена), поднял загадку на новый уровень, с помощью следующих рассуждений.
Игрок I играет L в узле 8, потому-что он знает, что Игрок II экономически рационален, и поэтому в узле 9 будет играть L, потому-что Игрок II тоже знает, что Игрок I экономически рационален, и поэтому в узле 10 готовится играть L. Но теперь у нас есть следующий парадокс: Игрок I должен предположить, что Игрок II в узле 9 предсказывает экономически рациональную игру Игрока I в узле 10, несмотря на то, что он дошёл до узла 9, который может быть достигнут только в том случае, если Игрок I не является экономически рациональным! А раз Игрок I не является экономически рациональным, то Игрок II не имеет оснований предсказывать, что Игрок I не будет играть R в узле 10, и в этом случае не ясно, что Игрок II не должен играть R в 9; и если Игрок II играет R в 9, то Игроку I гарантирован лучший выигрыш, чем он получит, если он сыграет L в узле 8. Оба игрока используют обратную индукцию для решения игры; обратная индукция требует, чтобы Игрок I знал, что Игрок II понял, что Игрок I является экономически рациональным; но Игрок II может решить эту игру только с помощью аргумента обратной индукции, которая допускает в качестве предпосылки неспособность Игрока I вести себя в соответствии с экономической рациональностью. Это и есть парадокс обратной индукции. Он напоминает нам о том, что не стоит всегда судить о других по себе: если лично Вы рациональны и у Вас всё в порядке с логикой - это отнюдь не значит, что оппонент способен мыслить теми же категориями.

Стандартный способ обойти этот парадокс "по справочнику" - использовать так называемую "слабую руку", термин предложенный Селтеном. Идея здесь в том, что решение и последующее действие могут "провалиться" с некоторой ненулевой вероятностью, какой бы малой эта вероятность ни была. То есть, игрок мог бы намереваться совершить действие, но затем ошибся в его выполнении, и вместо этого повёл игру по другому пути. Если есть хотя бы отдаленная вероятность того, что игрок может совершить ошибку - что его "рука может дрогнуть", - тогда не будет никакого противоречия, если игрок использует аргумент обратной индукции, который требует гипотетического предположения, что другой игрок пошёл по пути, который не позволяет соблюсти экономическую рациональность. В нашем примере Игрок II мог рассуждать о том, что делать в узле 9, при условии, что Игрок I выбрал L в узле 8, но затем допустил ошибку.
Гинтис указывает, что очевидный парадокс не возникает просто из нашего предположения об экономической рациональности обоих игроков. В его основе лежит дополнительная предпосылка о том, что каждый игрок должен знать и аргументировать, основываясь на знании того, что другой игрок является экономически рациональным. Это предпосылка, с которой несовместимы предположения каждого игрока о том, что может произойти при нарушении равновесия в игре. У игрока есть причина рассматривать возможности выхода из равновесия, если он либо считает, что его противник экономически разумен, но его рука может "дрогнуть", либо он приписывает некоторую ненулевую вероятность возможности того, что тот вообще не является экономически рациональным, или придаёт некоторое сомнение своей гипотезе о его функции полезности. Как ещё подчёркивает Гинтис, эта проблема с решением сложных игр для SEP с помощью алгоритма Цермело даёт обобщение: у игрока нет причин использовать даже стратегию равновесия по Нэшу, если он не ожидает, что другие игроки также будут играть по стратегии равновесия Нэша.
(Мы ещё вернемся к этому вопросу позже, поскольку он важен).

Парадокс обратной индукции, и загадки, возникающие при уточнении равновесия, - это в основном проблема для тех, кто рассматривает Теорию игр как вклад в нормативную теорию рациональности (в частности, как вклад в более широкую дисциплину - теорию стратегической рациональности).
Сторонник не-психологической Теории игр может дать иное объяснение явно "иррациональной" игры и той осторожности, которую она поощряет. Это связано с апелляцией к эмпирическому факту, что реальные агенты, включая людей, должны изучать стратегии равновесия игр, в которые они играют, по крайней мере, всякий раз, когда игры сложные. Исследования показывают, что даже такая простая игра, как "Дилемма заключенного", требует обучения людей (Camerer 2003 г.).
Сказать, что люди должны изучать стратегии равновесия, означает, что мы должны быть немного более изощрёнными, чем подразумевалось ранее, при построении функций полезности на основе поведения в применении теории выявленных предпочтений. Вместо того, чтобы строить функции полезности на основе отдельных эпизодов, мы должны делать это на основе наблюдаемых серий поведения, когда оно стабилизировалось, что означает зрелость обучения для рассматриваемых субъектов и рассматриваемой игры. И снова "Дилемма заключенного" является хорошим примером! Люди сталкиваются с немногими одноразовыми дилеммами заключенного в повседневной жизни, и они сталкиваются с множеством повторяющихся ДЗ с незнакомцами. В результате, когда в экспериментальной лаборатории обыгрывается единоразовая ДЗ, люди обычно начинают играть так, как если бы игра представляла собой лишь один раунд повторяющегося цикла ДЗ.
Повторяющаяся ДЗ, в свою очередь, имеет множество равновесий по Нэшу, предполагающих сотрудничество, а не предательство. Таким образом, экспериментальные субъекты сначала склонны сотрудничать в этих обстоятельствах, но после некоторого количества раундов учатся играть против правил. Экспериментатор не может сделать вывод о том, что он успешно вызвал одноразовое частичное разрешение с помощью своей экспериментальной модели, пока не удостоверится, что это поведение стабилизируется и повторяется.

Если игрок понимает, что другим игрокам может потребоваться изучить игровые структуры и равновесия на собственном опыте, это даёт ему повод принять во внимание то, что происходит на пути равновесия в играх с расширенными формами. Конечно, если игрок опасается, что другие игроки не научились равновесию, это вполне может лишить его стимула самому играть по стратегии равновесия. Осознание этого поднимает ряд глубоких проблем, связанных с социальным обучением (Fudenberg и Levine, 1998 г.).
Как неопытные игроки могут научиться соблюдать равновесие, если опытные игроки этого умышленно не демонстрируют? (потому-что искушённые не заинтересованы в игре по стратегии равновесия, пока неосведомлённые сами не научатся этому).
Ключевой ответ в случае применения Теории игр к взаимодействию между людьми состоит в том, что молодые люди социализируются, вырастая в сетях учреждений, включая изучение культурных норм. Самые сложные игры, в которые люди играют, развивались среди людей, которые были социализированы до них - то есть усвоили игровые структуры и равновесия раньше (Ross, 2008 г.).
Новички должны затем копировать только тех, чья игра кажется ожидаемой и понятной для других. Институты и жизненные нормы богаты напоминаниями, включая лекции и легко запоминаемые практические правила, чтобы помочь людям чётко понимать, что именно они делают (Clark, 1997 г.).
Как отмечалось в предыдущей публикации, когда наблюдаемое поведение не стабилизируется вокруг равновесия в игре, и нет свидетельств того, что обучение всё ещё продолжается, аналитик должен сделать вывод, что он неправильно смоделировал ситуацию, которую изучает. Скорее всего, он либо неверно указал функции полезности игроков, и стратегии, доступные игрокам, либо ошибся в догадках насчёт информации, которая им доступна. Учитывая сложность многих ситуаций, изучаемых социологами, мы не должны удивляться тому, что неправильная спецификация моделей случается часто.
В итоге, теоретики прикладных игр должны много обучаться на самой практике.

Парадокс обратной индукции - один из разряда таких парадоксов, которые возникают, если встраивать в концепцию рациональности владение и использование буквально полной информацией.
Вспомним по аналогии парадокс фондового рынка, который возникает, если мы предположим, что экономически рациональные инвестиции включают в себя буквально рациональные ожидания: предположим, что ни один индивидуальный инвестор не может обыграть рынок в долгосрочной перспективе, потому-что рынок всегда знает всё, что знает инвестор (плюс, ещё многое сверх этого); тогда никто не имеет стимула собирать информацию о стоимости активов; тогда никто и никогда не будет собирать такую информацию, потому-что исходит из предположения, что рынок знает всё, и его всё-равно не превзойти!
Как мы подробно увидим в различных обсуждениях далее, большая часть практического применения Теории игр явно включает неопределенность и перспективы обучения игроков. Игры с расширенной формой с SPE, которые мы рассмотрели ранее, являются действительно концептуальными инструментами, которые помогают нам подготовить формулировки для применения в ситуациях, когда полная и точная информация является необычной. Мы не сможем избежать парадокса, если будем думать, как некоторые философы и теоретики нормативных игр, что одним из концептуальных инструментов, которые мы хотим использовать для уточнения Теории игр, является полностью общая идея самой рациональности. Хотя, это не проблема для экономистов и других учёных, которые используют Теорию игр в эмпирическом моделировании.
В реальных случаях, если игроки не сталкивались с игрой в равновесии друг с другом в прошлом, даже если все они экономически рациональны и все доверяют друг другу, мы должны предугадать, что они добавят некоторую положительную вероятность к предположению, что понимание структуры игры среди некоторых игроков несовершенное. Это затем объясняет, почему люди, даже если они являются экономически рациональными агентами, могут часто (или даже чаще всего) играть так, будто они верят в "слабую руку".
Изучение равновесия может принимать различные формы для разных агентов и для игр разного уровня сложности и риска. Таким образом, включение его в теоретико-игровые модели взаимодействий вводит новый обширный набор технических особенностей. Наиболее полно разработанная общая теория рассмотрена у Fudenberg и Levine (1998 г.); те же авторы предоставили восемнадцатью годами позже дополнительный не-технический обзор проблем (2016 г.). Первое важное различие заключается в изучении конкретных параметров между раундами повторяющейся игры с общими игроками и изучении общих стратегических ожиданий в разных играх. Последнее может включать в себя изучение игроков, если обучающийся обновляет свои ожидания на основе своих моделей типов игроков, с которыми он периодически сталкивается. Затем мы можем провести различие между пассивным обучением, в котором игрок просто обновляет свои субъективные априорные знания, основываясь на наблюдении за ходами и результатами, плюс стратегическими выводами, которые он делает из них, и активным обучением, в котором он стремится получить информацию о стратегиях других игроков, выбирая те стратегии, которые проверяют его предположения о том, что произойдет на пути, который по его мнению является равновесным путём игры. Основная трудность как для игроков, так и для разработчиков моделей заключается в том, что ходы, сделанные ради "прощупывания", могут быть неверно истолкованы, если игроки также заинтересованы в том, чтобы делать ходы, ради передачи друг другу дезинформации. Другими словами: попытка "прощупать" стратегию может при некоторых обстоятельствах негативно повлиять на способности игроков изучать равновесие. Наконец, до сих пор обсуждение предполагало, что всё возможное обучение в игре связано со структурой самой игры. Wilcox в 2008 году доказал, что если игроки изучают новую информацию о казуальных процессах, происходящих вне игры, одновременно пытаясь обновить ожидания в отношении стратегий других игроков, разработчик моделей может обнаружить, что выходит за рамки текущих ограничений технических знаний.

Выше было сказано, что люди обычно могут играть так, будто верят в "слабые руки". Самая распространённая причина этого заключается в том, что когда люди взаимодействуют, мир не предоставляет им подсказок, открывающих всю структуру игр, в которые они играют. Они должны практиковаться и проверять предположения о своих догадках на практике, исходя из своего социального контекста. Иногда контексты фиксируются институциональными правилами. Например, когда человек заходит в розничный магазин и видит ценник на чем-то, что он хотел бы иметь, он знает, без необходимости гадать или узнавать что-либо, что он вовлечен в простую игру "бери или уходи". На других рынках он может знать, что от него ожидается торговля, и знает правила её проведения.
Учитывая неразрешённую сложную взаимосвязь между теорией обучения и Теорией игр, может показаться, что приведённое выше рассуждение подразумевает, что Теория игр никогда не может применяться к ситуациям с участием людей-игроков, для которых игра является новой и малоизученной. К счастью, мы не заходим в подобный тупик. В паре влиятельных работ середины и конца 1990-х годов Маккелви и Палфри (1995, 1998 г.) разработали концепцию учтения квантового равновесия реакции (QRE).
QRE не является усовершенствованием РН в том смысле, что это философски мотивированная попытка укрепить РН, посредством ссылки на нормативные стандарты рациональности. Это, скорее, метод расчёта равновесных свойств выбора, сделанного игроками, чьи предположения о возможных ошибках выбора у других игроков - не достоверны. Таким образом, QRE является стандартным механизмом в наборе инструментов экономистов-экспериментаторов, которые стремятся оценить распределение функций полезности в популяциях реальных людей, находящихся в ситуациях, смоделированных в виде игр. QRE не была практически пригодной для использования таким образом до тех пор, пока разработка эконометрических программ, таких как Stata™, позволила вычислять QRE с учётом достаточно объёмных записей статистики из интересных и сложных игр. QRE редко используется бихевиористскими экономистами и почти никогда не используется психологами при анализе лабораторных данных. Как следствие, многие исследования учёных этого типа содержат драматические риторические моменты, когда Капитан Очевидность "обнаруживает", что реальные люди часто не способны сходиться к РН в экспериментальных играх. И, хотя РН является минималистской концепцией решения в определенном смысле, поскольку оно абстрагируется от большей части информационной структуры, одновременно является требовательным эмпирическим ожиданием, если оно наложено категорически (то есть, если ожидается, что игроки будут играть так, как будто все они уверены, что все остальные играют по стратегии РН). Прогнозирование игры, согласованное с QRE, совпадает с точкой зрения о том, что РН отражает основную общую концепцию стратегического равновесия, и действительно мотивируется ею. Один из способов сформулировать философские отношения между РН и QRE заключается в следующем: РН определяет логический принцип, который хорошо приспособлен для дисциплины мышления и для разработки новых стратегий общего моделирования новых классов социальных явлений.
Для оценки реальных эмпирических данных необходимо уметь определять равновесие статистически. QRE представляет собой один из способов сделать это в соответствии с логикой РН. Идея настолько богата, что её глубины до сих пор остаются для Теоретиков игр открытой областью исследования. Текущее состояние понимания QRE всесторонне рассмотрено в труде J. Goeree, Holt and Palfrey "Квантовое равновесие реакции" (2016 г.).

📝 Богдан Карасёв, Scorum, 26 августа 2020 г., на основе материалов Стэнфордского университета.
✅ Уникальность статьи 100% (RU).
🎲 Анонс следующей публикации по Теории игр:
Неопределённость, риск и последовательное равновесие (материал будет опубликован в моём блоге между 28 августа и 5 сентября 2020 г.)
Комментарии