💼 Спонсор публикации: криптовалютная биржа EXMO >>>

В играх, которые мы моделировали до этого момента, все игроки выбирали среди чистых стратегий, в которых каждый ищет в каждом узле единственный оптимальный курс действий, который представляет собой лучший ответ на действия других.
Однако часто полезность игрока оптимизируется за счёт использования смешанной стратегии с подключением рандомизации, при которой он просто подбрасывает монетку для выбора среди нескольких возможных действий (позже мы увидим, что существует альтернативная интерпретация смешивания, не включающая рандомизацию в конкретном наборе информации; но сегодня начнём с интерпретации подбрасывания монеты / костей, а затем будем периодически использовать этот вариант и в следующих публикациях).
Смешивание стратегий требуется, когда нет чистой стратегии для максимизации полезности игрока против всех стратегий оппонента. Наша игра о переходе через реку из первой публикации проиллюстрировала это. Как мы увидели, загвоздка этой игры состоит в том, что, если рассуждения беглеца выбирают конкретный мост как оптимальный, следует предполагать, что его преследователь способен воспроизвести эту же цепочку рассуждений.
Но ведь беглец может сбежать только в том случае, если его преследователь не сможет достоверно предсказать, какой мост он использует! Таким образом, симметрия силы логических рассуждений двух игроков гарантирует, что беглец может удивить преследователя только в том случае, если он сможет удивить самого себя.

Предположим, что мы перестаём обращать внимание на камнепады и кобр на двух мостах, и представляем, что все мосты одинаково безопасны. Предположим также, что у беглеца нет специальных знаний о своём преследователе, которые могли бы побудить его отважиться на специально предполагаемое распределение вероятностей по доступным стратегиям преследователя. В этом случае лучший способ беглеца - бросить трехгранный кубик (кости), на котором каждая сторона представляет собой отдельный мост (или, ещё лучше, шестигранный кубик, в котором каждый мост представлен двумя сторонами). Затем он должен заранее взять на себя обязательство использовать любой мост, который выпадет по этому простому устройству рандомизации. Такой подход фиксирует шансы на его выживание, независимо от того, что сделает преследователь; но поскольку у преследователя нет причин отдавать предпочтение какой-либо доступной чистой или смешанной стратегии, и поскольку в любом случае мы предполагаем, что его эпистемическая ситуация симметрична ситуации беглеца, мы можем предположить, что он тоже бросит свои шестигранные кости. Теперь у беглеца есть 2/3 вероятности побега, а у преследователя - 1/3 вероятности его подстрелить. Ни беглец, ни преследователь не могут улучшить свои шансы, учитывая случайное сочетание выборов, поэтому обе стратегии рандомизации находятся в равновесии по Нэшу. Обратите внимание: если один игрок выполняет рандомизацию, то другой одинаково хорошо справляется с любым сочетанием вероятностей прохождения мостов, поэтому существует бесконечно много комбинаций лучших ответов. Однако, каждый игрок должен беспокоиться о том, что любая стратегия, кроме случайной, может быть скоординирована с каким-либо фактором, который другой игрок может обнаружить и использовать. Поскольку любая неслучайная стратегия может предугадаться другой неслучайной стратегией, в игре с нулевой суммой, такой как наш пример с мостами, то лишь вектор рандомизированных стратегий приводит к Равновесию Нэша (РН).

Теперь давайте повторно введём параметрические факторы, то есть падающие камни на мосту №2 и кобр на мосту №3. Опять же, предположим, что беглец обязательно 100% благополучно перейдёт через мост №1, имеет 90%-ную вероятность перехода через мост №2, не получив камнем по голове, и 80%-ную вероятность перехода через мост №3, не укушенным коброй. Мы сможем решить эту новую игру, если сделаем определенные предположения о функциях полезности двух игроков. Предположим, что Игрок 1 (беглец) заботится только о жизни или смерти (предпочитая, конечно, жизнь, а не смерть), в то время как Игрок 2 (преследователь) просто хочет, чтобы беглец умер, а не сбежал (другими словами, ни для одного из игроков не принципиально, каким путём беглец спасётся или каким именно способом умрёт). Предположим также, что ни один игрок не получает никакой пользы или потери от принятия большего или меньшего риска. В этом случае беглец просто берёт свою исходную формулу рандомизации и взвешивает её в соответствии с различными уровнями параметрической опасности на трёх мостах. Каждый мост следует рассматривать как лотерею по поводу возможных исходов беглеца, в которой каждая лотерея имеет различную ожидаемую выплату с точки зрения элементов его функции полезности.
Рассмотрим ситуацию с точки зрения преследователя. Он будет использовать свою стратегию РН, когда выберет сочетание вероятностей по трём мостам, которое делает беглеца равнодушным к выбору среди его возможных чистых стратегий. Мост с камнепадами для него в 1,1 раза опаснее безопасного моста. Следовательно, ему будет безразлично, какой из этих двух мостов выбрать, если в 1,1 раза больше шансов на то, что преследователь будет ждать у безопасного моста, чем у каменистого моста. Мост с кобрами в 1,2 раза опаснее для беглеца, чем безопасный мост. Следовательно, ему будет безразлично выбирать между этими двумя мостами, когда вероятность ожидания преследователем у безопасного моста в 1,2 раза выше, чем вероятность того, что он устроит засаду у моста с кобрами. Предположим, мы используем s1, s2 и s3 для представления параметрических показателей выживаемости беглеца на каждом мосту. Затем преследователь минимизирует чистую выживаемость на любой паре мостов, регулируя вероятности p1 и p2 того, что он будет ждать у них, так, чтобы s1 (1 − p1) было = s2 (1 − p2).
Поскольку p1 + p2 = 1, мы можем переписать формулу как:
s1 × p2 = s2 × p1
Или как:
p1/s1 = p2/s2
Таким образом, преследователь находит свою стратегию РН, решая следующие одновременные уравнения:
1 (1 − p1) = 0,9 (1 − p2)
= 0,8 (1 − p3)
p1 + p2 + p3 = 1
Затем:
p1 = 49/121
р2 = 41/121
p3 = 31/121
Теперь пусть f1, f2, f3 представляют вероятности, с которыми беглец выбирает каждый соответствующий мост.
Тогда беглец находит свою стратегию РН, решая уравнение:
s1 × f1 = s2 × f2
= s3 × f3
И далее:
1 × f1 = 0,9 × f2
= 0,8 × f3
Одновременно с:
f1 + f2 + f3 = 1
Потом:
f1 = 36/121
f2 = 40/121
f3 = 45/121
Эти два набора вероятностей РН говорят каждому игроку, как разметить свои "кости" перед тем, как их бросать. Обратите внимание на - возможно, удивительный - результат, заключающийся в том, что беглец (хотя гипотетически он не получает удовольствия от азартных игр), будет использовать более рискованные мосты с большей вероятностью. Так происходит, потому-что это единственный способ сделать для преследователя равнозначным, у какого моста ему поджидать, что, в свою очередь, увеличивает вероятность выживания беглеца.
Мы смогли решить эту игру напрямую, потому-что установили функции полезности таким образом, чтобы сделать её нулевой или строго конкурентной. То есть, каждый выигрыш в ожидаемой полезности одного игрока представляет собой точно симметричную потерю другого. Однако это условие часто может не выполняться.
Предположим теперь, что функции полезности более сложны. Преследователь больше всего предпочитает исход, при котором он стреляет в беглеца и, таким образом, берёт на себя ответственность за его уничтожение (личная месть), чем вариант, в котором тот умирает от упавшего камня или укуса змеи; хотя он и предпочтёт эти альтернативы его побегу. Беглец тоже предпочитает быструю смерть от пули, чем муки от ранения камнем или ужас от встречи с кобрами. Больше всего, конечно, он предпочтёт сбежать. Предположим, что беглец больше заботится о выживании, чем о том, чтобы его убили более "лёгким" способом. Мы не можем решить эту игру, как раньше, просто на основе знания порядковых функций полезности игроков, поскольку интенсивность их соответствующих предпочтений теперь будет влиять на их стратегии.
До работы фон Неймана и Моргенштерна (1947 г.) ситуации подобного рода по сути своей сбивали с толку аналитиков. Так происходило потому, что полезность не означает скрытую психологическую переменную, такую как, например, удовольствие. Мы уже обсудили ранее, что полезность - это просто мера относительных поведенческих диспозиций при определённых допущениях согласованности относительно соотношений между предпочтениями и выбором. Поэтому нет смысла сравнивать кардинальные, то есть чувствительные к интенсивности предпочтения наших игроков (личные предпочтения), поскольку не существует независимого, постоянного в межличностном отношении критерия, который мы могли бы использовать.
Как же тогда мы можем моделировать игры, в которых важна кардинальная информация? В конце концов, стало ясно, что моделирование игр требует одновременного учёта всех возможностей игроков.
Решающим аспектом трудов фон Неймана и Моргенштерна было решение этой проблемы. Здесь мы кратко опишем их гениальную технику построения кардинальных функций полезности из порядковых. Подчёркивается, что нижеследующее - это просто набросок, чтобы сделать кардинальную полезность не загадочной для человека, интересующегося философскими основами Теории игр и тем кругом проблем, к которым она может быть применена.
Предположим, что теперь мы назначаем беглецу, переходящему реку, следующую порядковую функцию полезности:
- Побег ≫ 4
- Смерть от пули ≫ 3
- Смерть от камнепада ≫ 2
- Смерть от укуса змеи ≫ 1
Мы предполагаем, что его предпочтение спасения от любой формы смерти сильнее, чем его предпочтения между выбором более "устраивающего" способа смерти. Это должно отразиться на его предпочтительном поведении следующим образом. В такой ситуации, как игра с переправой через реку, участник должен быть готов пойти на больший риск для увеличения относительной вероятности побега вместо его подстреления, чем для увеличения относительной вероятности получить пулю вместо укуса змеи. Эта часть логики является ключевым моментом в решении фон Нейманом и Моргенштерном проблемы кардинализации.
Предположим, мы попросили беглеца выбрать из доступного набора исходов лучший и худший. "Лучший" и "худший" определяются с точки зрения ожидаемых выплат, как показано в нашем текущем примере игры с нулевой суммой: игрок максимизирует свой ожидаемый выигрыш, если при выборе лотереи, содержащей только два возможных приза, он всегда выбирает такие варианты, которые максимизируют вероятность наилучшего результата - назовём это W - и минимизируют вероятность наихудшего результата - назовём это L. Теперь представьте, что Вы расширяете набор возможных призов так, чтобы он включал призы, которые агент считает промежуточными между W и L. Для набора результатов, содержащих такие призы, мы создаём лотерею по ним, включающую не только W и L. В нашем примере, это вариант, в котором беглеца застрелили быстро, а не раздавило в долгих муках под горными породами. Назовём этот вариант приза в лотерее T. Мы определяем функцию полезности q = u (T) от результатов до реальной (в отличие от порядковой) числовой строки так, что если q - ожидаемый приз в T, агенту безразлично между выигрышем T и выигрышем в лотерею T*, в которой W встречается с вероятностью u (T), а L встречается с вероятностью 1 - u (T). Если предположить, что поведение агента соответствует принципу сокращения составных лотерей (ROCL), то есть, когда игрок не получает и не теряет полезности от рассмотрения более сложных лотерей, а не простых, тогда набор отображений результатов в T в uT * даёт функция полезности Моргенштерна (vNMuf) с кардинальной структурой по всем исходам в T.
Что именно мы здесь сделали? Мы предоставили нашему агенту выбор в пользу лотереи, а не непосредственно в отношении решённых исходов, и наблюдали, насколько велик дополнительный риск смерти, который он готов предпринять, чтобы изменить шансы получить одну форму смерти по сравнению с альтернативной формой смерти. Обратите внимание, что это кардинализирует структуру предпочтений агента только по отношению к специфическим для агента контрольным точкам W и L; процедура ничего не раскрывает о сравнительных экстраординарных предпочтениях агентов, и это помогает прояснить, что построение vNMuf не вносит потенциально объективный психологический элемент. Более того, два агента в одной игре или один агент в разных обстоятельствах могут по-разному относиться к риску. Вероятнее всего, в игре с переходом через реку преследователь, чья жизнь не поставлена на карту, будет наслаждаться азартом игры в полную меру, в то время как беглец будет осторожничать. Однако, анализируя игру с переправой через реку, нам не обязательно сравнивать основные функции полезности преследователя и беглеца. В конце концов, оба агента могут найти свои стратегии РН, если они смогут оценить вероятности, которые каждый назначит действиям другого. Это означает, что каждый должен знать оба vNMufs; но им также не нужно пытаться сравнительно оценивать результаты, которые получит соперник в результате выбора.
Теперь мы можем заполнить оставшуюся часть матрицы игры с пересечением моста. Если оба игрока нейтральны к риску и их выявленные предпочтения соответствуют ROCL, то у нас есть достаточно информации, чтобы можно было определить ожидаемые полезности, выраженные путём умножения исходных выплат на соответствующие вероятности, как результаты в матрице. Предположим, что охотник ждёт у моста с кобрами с вероятностью Х, а возле каменистого моста с вероятностью Y. Поскольку все вероятности прохождения трёх мостов должны в сумме равняться 1, это означает, что он должен ждать у безопасного моста с вероятностью 1 - (X + Y). Затем, продолжая назначать беглецу вознаграждение 0, если он погибает, и 1, если он сбегает, а охотнику - обратные выплаты, наша полная матрица выглядит следующим образом:
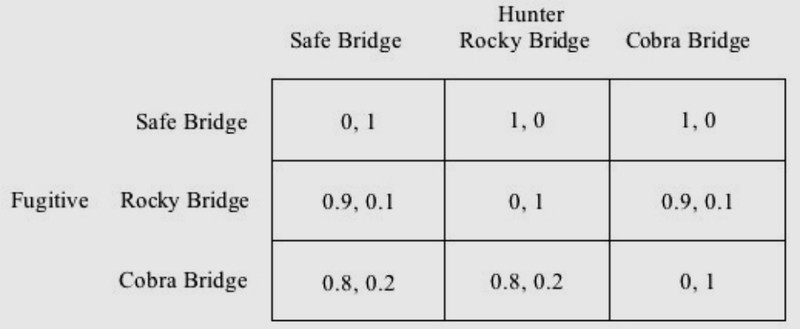
Теперь мы можем прочитать нужные факты и сделать вывод об игре прямо по матрице.
Вывод
Никакая пара чистых стратегий не является парой лучших альтернатив перед другими вариантами. Следовательно, только Равновесие Нэша в игре требует, чтобы хотя бы один игрок использовал смешанную стратегию.
📝 Богдан Карасёв, Scorum, 29 августа 2020 г., на основе материалов Стэнфордского университета.
✅ Уникальность статьи 100% (RU).
🎲 Анонс следующей публикации по Теории игр:
Убеждения и субъективные вероятности (материал будет опубликован в моём блоге между 2 и 9 сентября 2020 г.)
Комментарии